Dessa frågor ställdes av Per Enflo lördagen 22/2 2020 i Fokus B-sal, Östervåla,

i samband med att den polska TV-dokumentären "Banach. MIĘDZY DUCHEM A MATERIĄ." (Banach. Mellan ande och materia) visades för släkt och vänner

1. Det tar ca 365,24 dagar för jorden att gå ett varv runt solen. Så vi låter året ha 365 och ibland 366 dagar (skottår) för att det ska bli rätt.

Vår kalender ger ett fel på 1 dag efter ca 3.000 år. Det betyder ungefär 30 sek. fel/år. Iraniern Omar Khayyam (1048-1123) fick år 1080 uppdraget att göra en ny kalender. Efter 18 år var uppdraget klart.

Hur exakt är Omars kalender?

Det blir en dag fel efter

(A) 200 år (ungefär 7 ½ minut fel/år)

(B) 1.000 år (ungefär 1 ½ minut fel/år)

Åren omkring 700 - 1200 e.Kr. låg centrum för vetenskap i mellanöstern med Bagdad som en betydande plats. Antikens böcker översattes och bevarades. Omar Khayyam var en av de verkligt stora. Han förde matematiken vidare med bl.a. omfattande studier av ekvationer av tredje graden. Han var också poet. I briljanta 4-radiga verser, s.k. rubaiyat, uttrycker han ofta att vi måste ta vara på det kanske enda liv vi har. I en hänvisar han till sin kalender när han talar med en vän:

Men min astronomi, ger du till svar,

en bättre tideräkning skapat har.

Ja, forntid strök jag bort ur min kalender

och framtid - tills blott nuet levde kvar

Rätt svar: C

Omars kalender är alltså mer exakt än den kalender vi använder. Den används idag i Iran. Nyåret inträffar vid vårdagjämningen. Dock, sättet att räkna ut vilka år som får vara skottår är något mer komplicerat än för den gregorianska kalendern.

2. Eftersom stjärnhimlen ändrar sig när man kommer närmare ekvatorn visste man redan under antiken att jorden är rund.

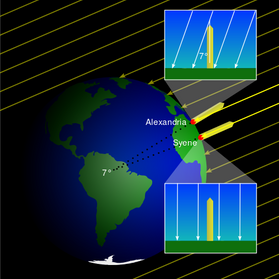
På 200-talet f.Kr försökte greken Eratosthenes (som levde 276-194 f.Kr) att mäta omkretsen med hjälp av observationen att när solen stod i zenit i Assuan, stod den 7,2 grader från zenit i Alexandria, knappt 80 mil därifrån.

Idag vet vi att omkretsen är 4.000 mil, och vilken omkrets kom Eratosthenes fram till?

(A) 2.348 mil

(B) 3.936 mil

Rätt svar: B

Eratosthenes uppskattning är alltså mycket nära den rätta. Man ser ibland andra siffror än 3936 mil. Jag tror att detta beror på att det är svårt att exakt ange vilken uppskattning Eratosthenes hade av avståndet mellan Assuan och Alexandria.

Vilket år gjorde Columbus sin resa?

(A) 1392

(B) 1442

3. Christofer Columbus (1451-1506) använde kunskapen att jorden är rund. För att komma till Indien, resonerade han, behöver man därför inte åka österut som man alltid gjort tidigare. Om man åker västerut måste man ju också till sist komma till Indien. Så han gjorde det, på vägen stötte han på Amerika, som då blev återupptäckt av européerna.

Rätt svar: C

4. Ole Rømer (1644 - 1710), en dansk astronom och ämbetsman, var den förste som mätte ljusets hastighet redan år 1676. Rømer observerade att tiden för Jupiters måne Io att fullborda 40 varv runt Jupiter - drygt två månader - tycktes minska med 22 minuter då jorden närmade sig Jupiter jämfört med när jorden avlägsnar sig från Jupiter. Han kom fram till hastigheten 22 000 mil/sek , och med bättre kunskap om de astronomiska avstånden hade han kommit ännu närmare den korrekta siffran 30 000 mil/sek. Viktigare än den exakta siffran var den stora upptäckten att ljusets hastighet inte är oändlig som greken Aristoteles 2 000 år tidigare hade sagt. Rømers resultat var några hundra år före sin tid.

När kom man fram till mer exakt uppskattning av ljusets hastighet?

(A) 1849 (Foucault - Fizeau´s experiment)

(B) 1865 (Maxwell´s studier av elektromagnetism)

Rätt svar: A

Foucault -Fizeau´s experiment gjordes med hjälp av ett snabbt roterande kugghjul och en avlägsen spegel. När en ljussignal skickades mot spegeln genom ett hål i kugghjulet, släpptes den på tillbakavägen också igenom ett hål i kugghjulet, om detta roterade med rätt hastighet.

Kommentar: (B) Maxwell visade att elektromagnetiska vågor och ljusvågor liknar varandra och (C) Michelson -Morley’s experiment visade att ljuset går lika fort i alla riktningar, vare sig ljuskällan rör sig eller ej. (B) och (C) är viktiga som bakgrund till Einsteins Relativitetsteori.

Finns det hur stora primtalstvillingar som helst?

(A) Ja (B) Nej (C) Vet ej

Och namnet Ada lever kvar i programspråket ADA från 1980-talet.

ADA programspråk skapades:

(A) för USA’s försvarsdepartement

(B) vid Ecole Polytechnique, Paris

5. Ett PRIMTAL är ett naturligt tal, som är större än 1 och som inte har några andra delare än 1 och talet självt.

Exempel: 7 är ett primtal eftersom det bara är delbart med 7 och med 1.

6 är inget primtal eftersom 6 är delbart med 2 och med 3. 35 är inget primtal då det är delbart med 5 och med 7.

11 , 13 , 17 och 19 är primtal. 65537 är ett primtal.

Finns det hur stora primtal som helst? Ja, och det bevisades redan under antiken. Euklides skrifter innehåller ett elegant bevis. "Eratosthenes' såll" är en enkel metod att vaska fram primtal. I över 2 000 år hade primtalen huvudsakligen intresse för teoretiker och talmystiker. Men i och med datorernas utveckling är de nu av största praktiska betydelse för kryptering och säkerhetssystem, t.ex i banker.

Primtalstvillingar är par av udda primtal, som ligger intill varandra, på bilden ovan har primtalen röda siffror. Exempel: (11,13), (17,19), (29,31), (101,103) är primtalstvillingar.

Rätt svar: C Vet ej.

Allt tyder på att det finns hur stora primtalstvillingar som helst, men det finns inget bevis ännu. De första framstegen på problemet gjordes av norrmannen Viggo Brun, som 1915 med en förbättring av Eratosthenes´ såll, visade att det finns hur stora talpar (n, n+2) som helst där n och n+2 är produkter av högst 9 primtal. Detta har sedan förbättras till att n är ett primtal och n+2 är en produkt av högst 2 primtal. 2013 visade Zhang att det finns hur stora primtalspar (p, p+r) som helst där r är högst 70.000.000. Detta har sen förbättras till att r är högst 246. Men för r=2, finns, som sagt, ännu inget bevis.

6. Ada Lovelace (1815 - 1852 )

I England vid 1800-talets mitt kom matematikern Lady Ada, grevinna av Lovelace och dotter till poeten Lord Byron, redan vid 18 års ålder att fascineras av de maskiner som matematikern Charles Babbage (1791 - 1871) skissat fram. För honom var hans differensmaskin, och sedan den analytiska maskinen, bara räknemaskiner för avancerade matematiska uppgifter. Ada Lovelace gick vidare och beskrev 1842 en algoritm för hur Babbage-maskinen skulle utföra sina beräkningar, något som betecknats som världens första datorprogram.

Hon utvecklade också en vision om datorers potential till att inte bara producera siffror. Hon beskrev sitt arbetssätt som "poetisk vetenskap" och sig själv som analytiker & metafysiker, med frågeställningar kring den analytiska maskinen som rörde relationen mellan människa och samhälle å ena sidan och tekniken som ett redskap å den andra. I framtiden skulle datorer inte bara kunna programmeras för godtyckliga beräkningsuppgifter, utan även rita, skriva och skapa musik.

Charles Babbage och Ada Lovelaces arbeten har förblivit en teoretisk produkt, så koden har än så länge inte kunnat testas i praktiken.

Rätt svar: A

USA:s försvarsdepartement ville rensa i floran av programspråk som användes för alla de system som fanns inom de olika försvarsgrenarna i slutet av 1970-talet.

7. Sonja Kovalevsky (1850 - 1891)

Sonja Kovalevsky föddes i Moskva, växte delvis upp i St Petersburg, och påbörjade där tidigt studier i matematik. Hon fortsatte studierna i Tyskland och fick doktorsgrad 1874. 1881 flyttade hon till Sverige, där hon 1884 blev professor i matematik vid Stockholms Högskola. Hon var den första kvinnliga professorn i Sverige (i ngt ämne öht). Hennes mest kända arbete är " Om en fast kropps rotation kring en fast punkt". För detta belönades hon 1888 med det prestigefyllda franska Bordin-priset, och på grund av arbetets höga kvalitet erhöll hon den dubbla prissumman.

Det finns en film om henne som heter

(A) A beautiful mind (B) Berget på månens baksida (C) A mathematician's apology

Rätt svar: B

Berget på månens baksida. Sonja Kovalevsky lär ha sagt ungefär att om hon lyckades i matematik kunde hon få ett berg på månens baksida uppkallat efter sig. Hon har fått en krater på månens baksida uppkallad efter sig. Detsamma gäller den svenske matematikern Ivar Fredholm, vars upptäckter omkr. 1900 var viktiga bl.a. som bakgrund för funktionalanalysen.

Kommentar: (A) är en bok (och film) om matematikern John Nash, som 1994 fick nobelpris i ekonomi för sina upptäckter, men som också led av schizofreni. (C) är en skrift av matematikern Godfrey Hardy (1877 - 1947). Han lär ha sagt ”Jag har aldrig gjort något nyttigt”. I skriften förklarar han varför han ändå ägnat sig åt matematik. Hans resultat har haft viktiga tillämpningar.

Och nu till våra polska vetenskapare:

8. Marie Skłodowska Curie, mest känd som Marie Curie (1867 - 1934), född i Warszawa, gjorde banbrytande insatser inom radioaktivitet och radioaktiva ämnen. Hennes upptäckter har, genom alla tillämpningar, varit av den största betydelse för hela vårt moderna samhälle.

Hon fick nobelpris i två olika vetenskapliga områden, i fysik år 1903 och i kemi år 1911. I fysik för banbrytande forskning om radioaktivitet, i kemi för upptäckten av grundämnena radium och polonium (i mineralet uraninit). En bakgrund till den sista upptäckten var upptäckten att mineralet uraninit var mer radioaktivt än det uran som utvanns därur. Grundämnet Curium är uppkallat efter Marie Curie och måttenheten Curie

Har någon, förutom Marie Curie, fått nobelpris i två olika vetenskapliga områden? (A) Ja (B) Nej

Rätt svar: B nej

Den enda person förutom Marie Curie, som fått 2 nobelpris i olika kategorier är Linus Pauling, som fick kemipriset år 1954 och fredspriset år 1962. John Bardeen fick två nobelpris i fysik, 1956 och 1972, och Frederick Sanger fick 2 nobelpris i kemi, 1958 och 1980.

9. Nicolaus Copernicus (1473 - 1543) Copernicus är mest känd för den heliocentriska världsbilden - att solen är det centrum, som jorden och de övriga planeterna kretsar runt. Han var ett universalsnille. Han formulerade flera grundläggande ekonomiska lagar, som sedan återupptäcktes på 1700- och 1800-talen, och han var läkare, diplomat, jurist, militärstrateg m.m.

Vid vilka universitet studerade Copernicus?

obs! alla tre städerna måste vara rätt!

(A) Krakow, Warszawa och Lwow

(B) Krakow, Bologna och Padua

Rätt svar: B

10. Stefan Banach (1892 - 1945) Stefan Banach är en av 1900-talets mest inflytelserika matematiker, och en förgrundsgestalt i skapandet av funktionalanalysen, som har stor betydelse i vårt moderna samhälle. Han är, tillsammans med Nicolaus Copernicus och Marie Curie, en av Polens, genom tiderna, mest framstående vetenskapsmän. Men till skillnad från Copernicus och Curie är han fortfarande ganska okänd för de flesta. Ett syfte med TV-dokumentären om honom, är att göra honom och hans betydelse mer bekant för en större allmänhet.

En av funktionalanalysens grundläggande satser är Hahn - Banachs teorem, som är en långtgående generalisering av någonting ganska självklart: Om man ritar två konvexa figurer på ett papper (”konvex” betyder att de inte har någon inbuktning) och dessa figurer inte har någon gemensam punkt, då kan man dra en linje, så att figurerna ligger på varsin sida av linjen.

Vad kan Hahn - Banachs teorem användas för?

(A) Prissättning av aktier och obligationer.

(B) Teori för att få optimalt resultat i en beslutssituation.

Rätt svar: A och B och C,

dvs inom alla tre områden!